Widening
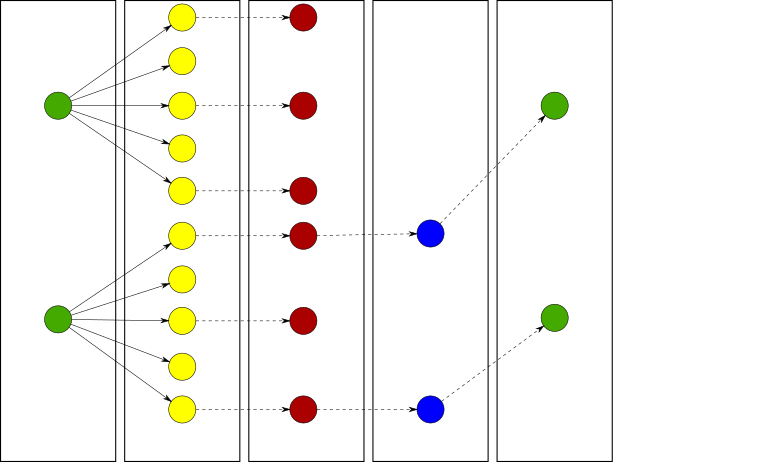
Widening is an improvement for greedy algorithms that learn a model by iteratively refining it. Instead of utilizing parallel compute resources to make algorithms faster, widening aims to find better solutions by covering the search space more broadly. Widening consists of two major steps: refinement and selection. Refinement is the process of taking an existing, potentially incomplete, model and generate possible successors by changing its parameters. An example for this is the merge step of hierarchical clustering, where in each step a number of potential merges is available. In the selection step, where a greedy algorithm would select the best model according to a heuristic, we select multiple models in widening. Applied to the clustering example this means selecting multiple merges and continue with the resulting models in parallel. An important criteria for the selection is that the selected models are not only good, but also diverse, to ensure broad coverage of the search space.
Challenges in widening algorithms lie in the efficient enforcement of diversity among the explored models and the fact that communication between the parallel workers should be limited.
We applied widening to various algorithms and have published the following papers in this area:
- Parallel Data Mining Revisited. Better, Not Faster
- Diversity-Driven Widening
- Diversity-driven Widening of Hierarchical Agglomerative Clustering
- Bucket Selection: A Model-Independent Diverse Selection Strategy for Widening
- Widened KRIMP: better performance through diverse parallelism
- Widened Learning of Bayesian Network Classifiers
The Bucket Selector
Our latest contribution is the bucket selector, a model-independent randomized selection strategy that can be applied to join order optimization, set covering and hierarchical clustering.
The bucket selector works as follows:
If we have k workers, each worker is assigned a hash value between 1 and k. The bucket selector first hashes each object locally on each parallel worker into k buckets and keeps the best model from each bucket. Now the workers exchange models, each worker sending the best model of a bucket to the corresponding worker, which can then select the overall best model in the bucket and refine it.
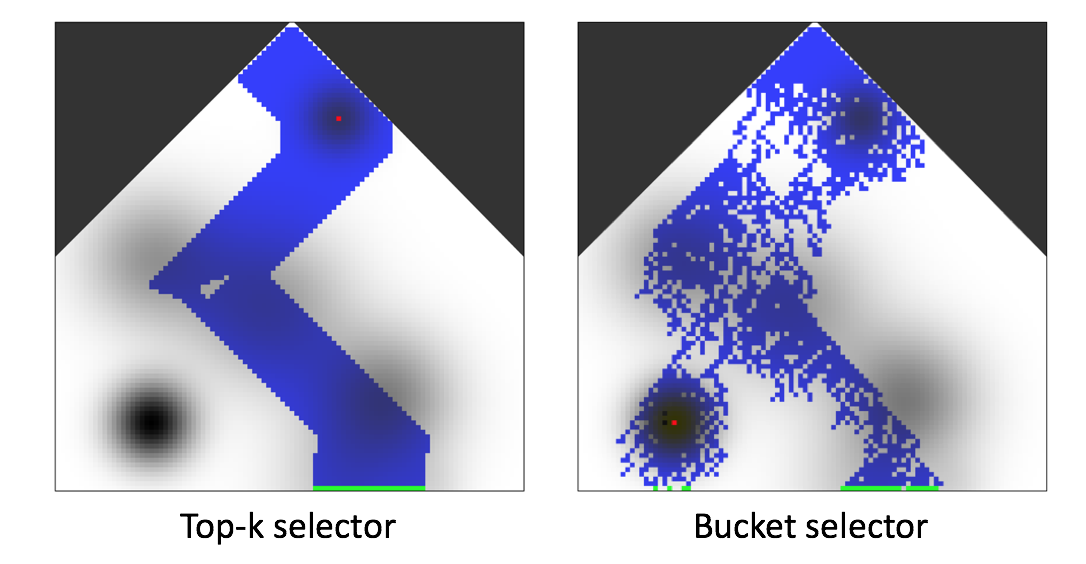
The image below shows how the bucket selector explores a toy model space more broadly than the naive top-k selector that does not enforce diversity and simply selects the k best models.
Bayesian Networks
Diversity selection in this method has the drawback that it is computationally intensive and resistant to parallelization. Further research is focused on completely parallelizable methods of compute workers searching through diverse partitions of the solution space.
Learning Bayesian networks from datasets for use as classifiers involves refining and selecting models within an enormous solution space. To this end, the use of a distance measure, the Frobenius Norm of the unnormalized Graphs Laplacian of the undirected graphs, has proven fruitful. During the refining step, groups of diverse models are selected using the p-dispersion-min-sum measure, and are then selected based on their classification performance.
Initial models (green, left) are refined (yellow) from which the most diverse (red) are found. The best of these (blue) are selected and are then used for the next iteration (green, right).